Initial Guesses Subpackage¶

Inheritance Diagram¶

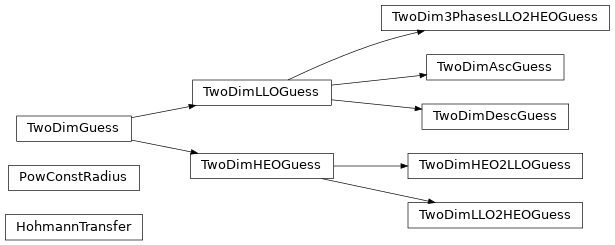
Modules List¶

`latom.guess.guess_2d`	@authors: Alberto FOSSA’ Giuliana Elena MICELI
`latom.guess.guess_heo_2d`	@authors: Alberto FOSSA’ Giuliana Elena MICELI

Documentation¶

@authors: Alberto FOSSA’ Giuliana Elena MICELI

class latom.guess.guess_2d.HohmannTransfer(gm, dep, arr)[source]

Bases: object

HohmannTransfer class implements a two-dimensional Hohmann transfer between two coplanar, circular orbits in the Keplerian two-body approximation.

Parameters

gm (float) – Standard gravitational parameter of the central attracting body [m^3/s^2]
dep (TwoDimOrb) – TwoDimOrb class instance representing the departure orbit
arr (TwoDimOrb) – TwoDimOrb class instance representing the arrival orbit

Variables

GM (float) – Standard gravitational parameter of the central attracting body [m^3/s^2]
dep (TwoDimOrb) – TwoDimOrb class instance representing the departure orbit
arr (TwoDimOrb) – TwoDimOrb class instance representing the arrival orbit
ra (float) – Transfer orbit apoapsis radius [m]
rp (float) – Transfer orbit periapsis radius [m]
transfer (TwoDimOrb) – TwoDimOrb class instance representing the transfer orbit
tof (float) – Hohmann transfer time of flight corresponding to half of the transfer period [s]
dvp (float) – Impulsive delta-V at periapsis [m/s]
dva (float) – Impulsive delta-V at apoapsis [m/s]
r (ndarray) – Radius time series for the transfer arc [m]
theta (ndarray) – Angle time series for the transfer arc [rad]
u (ndarray) – Radial velocity time series for the transfer arc [m/s]
v (ndarray) – Tangential velocity time series for the transfer arc [m/s]
states (ndarray) – States variables time series for the transfer arc as [r, theta, u, v, m]
controls (ndarray) – Control variables time series for the transfer arc as [thrust, alpha]

compute_trajectory(t, t0=0.0, theta0=0.0, m=1.0)[source]

Computes the states and control time series along the transfer trajectory.

Parameters

t (ndarray) – Time vector [s]
t0 (float) – Initial time [s]
theta0 (float, optional) – Initial angle. Default is 0.0 [rad]
m (float) – Spacecraft mass. Default is 1.0 [kg]

Returns

root – Solution of the Kepler time of flight equation for the eccentric anomaly in function of the true anomaly

Return type

ndarray

class latom.guess.guess_2d.PowConstRadius(gm, r0, v0, vf, m0, thrust, isp, theta0=0.0, t0=0.0)[source]

Bases: object

PowConstRadius class implements a two-dimensional powered phase at constant radius from the central attractive body.

The trajectory is modeled in the restricted two-body problem framework and the spacecraft engines are supposed to deliver a constant thrust magnitude across the whole phase. Since the radius r is constant, the radial velocity u is always null.

Parameters

gm (float) – Central body standard gravitational parameter [m^3/s^2]
r0 (float) – Radius [m]
v0 (float) – Initial tangential velocity [m/s]
vf (float) – Final tangential velocity [m/s]
m0 (float) – Initial spacecraft mass [kg]
thrust (float) – Thrust magnitude [N]
isp (float) – Specific impulse [s]
theta0 (float) – Initial angle [rad]
t0 (float) – Initial time [rad]

Variables

GM (float) – Central body standard gravitational parameter [m^3/s^2]
R (float) – Radius [m]
v0 (float) – Initial tangential velocity [m/s]
vf (float) – Final tangential velocity [m/s]
m0 (float) – Initial spacecraft mass [kg]
T (float) – Thrust magnitude [N]
Isp (float) – Specific impulse [s]
theta0 (float) – Initial angle [rad]
t0 (float) – Initial time [rad]
dv_inf (float) – Delta-V required to accelerate the spacecraft from v0 to vf assuming an impulsive burn [m/s]
tf (float) – Final time [s]
thetaf (float) – Final angle [rad]
mf (float) – Final spacecraft mass [kg]
dv (float) – Delta-V required to accelerate the spacecraft from v0 to vf taking into account a finite thrust magnitude equal to T [m/s]
t (ndarray) – Time vector [s]
r (ndarray) – Radius time series [m]
theta (ndarray) – Angle time series [rad]
u (ndarray) – Radial velocity time series [m/s]
v (ndarray) – Tangential velocity time series [m/s]
m (ndarray) – Spacecraft mass time series [kg]
alpha (ndarray) – Thrust direction time series [rad]
states (ndarray) – States variables time series as [r, theta, u, v, m]
controls (ndarray) – Controls variables time series as [thrust, alpha]

compute_mass(t)[source]

Compute the spacecraft mass time series.

Parameters: t (ndarray) – Time vector [s]
Returns: m – Spacecraft mass time series [kg]
Return type: ndarray

compute_final_time_states()[source]

Compute the required time of flight and the final spacecraft states.

Returns

sol_time (tuple) – Solution of the Initial Value Problem (IVP) for the final time. See scipy.integrate.solve_ivp for more details
sol_states (tuple) – Solution of the Initial Value Problem (IVP) for the final angle and speed. See scipy.integrate.solve_ivp for more details

compute_trajectory(t_eval)[source]

Compute the spacecraft states and controls variables time series across the powered phase.

Parameters: t_eval (ndarray) – Time vector in which the states and controls are provided [s]
Returns: sol – Solution of the Initial Value Problem (IVP) for the final time. See scipy.integrate.solve_ivp or scipy.integrate.odeint for more details
Return type: tuple or dict

dt_dv(v, t, gm, r, m0, t0, thrust, isp)[source]

ODE for the first derivative of the time t wrt the tangential velocity v.

Parameters

v (float or ndarray) – Tangential velocity time series [m/s]
t (float or ndarray) – Time vector [s]
gm (float) – Central body standard gravitational parameter [m^3/s^2]
r (float or ndarray) – Radius time series [m]
m0 (float) – Initial spacecraft mass [kg]
t0 (float) – Initial time [s]
thrust (float) – Thrust magnitude [N]
isp (float) – Specific impulse [s]

Returns

dt_dv – First derivative of t wrt v [s^2/m]

Return type

float or ndarray

dv_dt(t, v, gm, r, m0, t0, thrust, isp)[source]

ODE for first time derivative of the tangential velocity v.

Parameters

t (float or ndarray) – Time vector [s]
v (float or ndarray) – Tangential velocity time series [m/s]
gm (float) – Central body standard gravitational parameter [m^3/s^2]
r (float or ndarray) – Radius time series [m]
m0 (float) – Initial spacecraft mass [kg]
t0 (float) – Initial time [s]
thrust (float) – Thrust magnitude [N]
isp (float) – Specific impulse [s]

Returns

dv_dt – First time derivative of v [m/s^2]

Return type

float or ndarray

dx_dt(t, x, gm, r, m0, t0, thrust, isp)[source]

Systems of ODEs for the first time derivatives of the angle theta and the tangential velocity v.

Parameters

t (float or ndarray) – Time vector [s]
x (ndarray) – Angle and tangential velocity time series as [theta, v] [rad, m/s]
gm (float) – Central body standard gravitational parameter [m^3/s^2]
r (float or ndarray) – Radius time series [m]
m0 (float) – Initial spacecraft mass [kg]
t0 (float) – Initial time [s]
thrust (float) – Thrust magnitude [N]
isp (float) – Specific impulse [s]

Returns

x_dot – First time derivatives of theta and v [rad/s, m/s^2]

Return type

ndarray

class latom.guess.guess_2d.TwoDimGuess(gm, r, dep, arr, sc)[source]

Bases: object

TwoDimGuess provides an initial guess for a two-dimensional transfer trajectory combining powered phases at constant radius with Hohmann transfer arcs.

Parameters

gm (float) – Central body standard gravitational parameter [m^3/s^2]
r (float) – Central body equatorial radius [m]
dep (TwoDimOrb) – Departure orbit object
arr (TwoDimOrb) – Arrival orbit object
sc (Spacecraft) – Spacecraft object

Variables

GM (float) – Central body standard gravitational parameter [m^3/s^2]
R (float) – Central body equatorial radius [m]
dep (TwoDimOrb) – Departure orbit object
ht (HohmannTransfer) – HohmannTransfer object
t (ndarray) – Time vector [s]
states (ndarray) – States time series as [r, theta, u, v, m]
controls (ndarray) – Controls time series as [thrust, alpha]

class latom.guess.guess_2d.TwoDimLLOGuess(gm, r, dep, arr, sc)[source]

Bases: latom.guess.guess_2d.TwoDimGuess

TwoDimLLOGuess provides an initial guess for a two-dimensional ascent or descent trajectory from the Moon surface to a circular Low Lunar Orbit.

The approximate transfer consists into two powered phases at constant radius and an Hohmann transfer.

Parameters

gm (float) – Central body standard gravitational parameter [m^3/s^2]
r (float) – Central body equatorial radius [m]
dep (TwoDimOrb) – Departure orbit object
arr (TwoDimOrb) – Arrival orbit object
sc (Spacecraft) – Spacecraft object

Variables

pow1 (PowConstRadius) – First powered phase at constant radius
pow2 (PowConstRadius) – Second powered phase at constant radius

compute_trajectory(fix_final=False, **kwargs)[source]

Computes the states and controls time series for a given time vector or number of equally space nodes.

Parameters

fix_final (bool, optional) – True if the final angle is fixed, False otherwise. Default is False

Other Parameters

t_eval (ndarray) – Time vector in which states and controls are computed [s]
nb_nodes (int) – Number of equally space nodes in time in which states and controls are computed

class latom.guess.guess_2d.TwoDimAscGuess(gm, r, alt, sc)[source]

Bases: latom.guess.guess_2d.TwoDimLLOGuess

TwoDimAscGuess provides an initial guess for a two-dimensional ascent trajectory from the Moon surface to a circular LLO.

The approximate transfer comprises a first powered phase at constant radius equal to the Moon one, an Hohmann transfer and a second powered phase at constant radius equal to the LLO one.

Parameters

gm (float) – Central body standard gravitational parameter [m^3/s^2]
r (float) – Central body equatorial radius [m]
alt (float) – LLO altitude [m]
sc (Spacecraft) – Spacecraft object

Variables

pow1 (PowConstRadius) – First powered phase at constant radius
pow2 (PowConstRadius) – Second powered phase at constant radius
tf (float) – Final time [s]

compute_trajectory(fix_final=False, **kwargs)

Computes the states and controls time series for a given time vector or number of equally space nodes.

Parameters

fix_final (bool, optional) – True if the final angle is fixed, False otherwise. Default is False

Other Parameters

t_eval (ndarray) – Time vector in which states and controls are computed [s]
nb_nodes (int) – Number of equally space nodes in time in which states and controls are computed

class latom.guess.guess_2d.TwoDimDescGuess(gm, r, alt, sc)[source]

Bases: latom.guess.guess_2d.TwoDimLLOGuess

TwoDimDescGuess provides an initial guess for a two-dimensional descent trajectory from a circular LLO to the Moon surface.

The approximate transfer comprises a first powered phase at constant radius equal to the LLO one, an Hohmann transfer and a second powered phase at constant radius equal to the Moon one.

Parameters

gm (float) – Central body standard gravitational parameter [m^3/s^2]
r (float) – Central body equatorial radius [m]
alt (float) – LLO altitude [m]
sc (Spacecraft) – Spacecraft object

Variables

pow1 (PowConstRadius) – First powered phase at constant radius
pow2 (PowConstRadius) – Second powered phase at constant radius
tf (float) – Final time [s]

compute_trajectory(fix_final=False, **kwargs)

Computes the states and controls time series for a given time vector or number of equally space nodes.

Parameters

fix_final (bool, optional) – True if the final angle is fixed, False otherwise. Default is False

Other Parameters

t_eval (ndarray) – Time vector in which states and controls are computed [s]
nb_nodes (int) – Number of equally space nodes in time in which states and controls are computed

@authors: Alberto FOSSA’ Giuliana Elena MICELI

class latom.guess.guess_heo_2d.TwoDimHEOGuess(gm, r, dep, arr, sc)[source]

Bases: latom.guess.guess_2d.TwoDimGuess

TwoDimHEOGuess provides an initial guess for an LLO to HEO transfer or vice-versa.

The approximate trajectory comprises a powered phase at constant radius, an Hohmann transfer and an impulsive burn.

Parameters

gm (float) – Central body standard gravitational parameter [m^3/s^2]
r (float) – Central body equatorial radius [m]
dep (TwoDimOrb) – Departure orbit object
arr (TwoDimOrb) – Arrival orbit object
sc (Spacecraft) – Spacecraft object

Variables

pow (PowConstRadius) – PowConstRadius object

compute_trajectory(**kwargs)[source]

Computes the states and controls timeseries on the provided time grid.

Other Parameters

t_eval (ndarray) – Time vector in which states and controls are computed [s]
nb_nodes (int) – Number of equally space nodes in time in which states and controls are computed

class latom.guess.guess_heo_2d.TwoDimLLO2HEOGuess(gm, r, alt, rp, t, sc)[source]

Bases: latom.guess.guess_heo_2d.TwoDimHEOGuess

TwoDimLLO2HEOGuess provides an initial guess for an LLO to HEO transfer.

The approximate trajectory comprises a powered phase at constant radius equal to the LLO one, an Hohmann transfer and an impulsive burn at the HEO apoapsis.

Parameters

gm (float) – Central body standard gravitational parameter [m^3/s^2]
r (float) – Central body equatorial radius [m]
alt (float) – LLO altitude [m]
rp (float) – HEO periapsis radius [m]
t (float) – HEO period [s]
sc (Spacecraft) – Spacecraft object

Variables

pow (PowConstRadius) – PowConstRadius object
tf (float) – Final time [s]
insertion_burn (ImpulsiveBurn) – ImpulsiveBurn object

compute_trajectory(fix_final=True, throttle=True, **kwargs)[source]

Computes the states and controls timeseries on the provided time grid.

Parameters

fix_final (bool, optional) – True if the final angle is fixed, False otherwise. Default is True
throttle (bool, optional) – If True replace the spacecraft states on the last node with the ones from ImpulsiveBurn

Other Parameters

t_eval (ndarray) – Time vector in which states and controls are computed [s]
nb_nodes (int) – Number of equally space nodes in time in which states and controls are computed

class latom.guess.guess_heo_2d.TwoDimHEO2LLOGuess(gm, r, alt, rp, t, sc)[source]

Bases: latom.guess.guess_heo_2d.TwoDimHEOGuess

TwoDimHEO2LLOGuess provides an initial guess for an HEO to LLO transfer.

The approximate trajectory comprises an impulsive burn at the HEO apoapsis, an Hohmann transfer and a powered phase at constant radius equal to the LLO one.

Parameters

gm (float) – Central body standard gravitational parameter [m^3/s^2]
r (float) – Central body equatorial radius [m]
alt (float) – LLO altitude [m]
rp (float) – HEO periapsis radius [m]
t (float) – HEO period [s]
sc (Spacecraft) – Spacecraft object

Variables

pow (PowConstRadius) – PowConstRadius object
tf (float) – Final time [s]
deorbit_burn (ImpulsiveBurn) – ImpulsiveBurn object

compute_trajectory(**kwargs)[source]

Computes the states and controls timeseries on the provided time grid.

Other Parameters

t_eval (ndarray) – Time vector in which states and controls are computed [s]
nb_nodes (int) – Number of equally space nodes in time in which states and controls are computed

class latom.guess.guess_heo_2d.TwoDim3PhasesLLO2HEOGuess(gm, r, alt, rp, t, sc)[source]

Bases: latom.guess.guess_2d.TwoDimLLOGuess

TwoDim3PhasesLLO2HEOGuess provides an initial guess for a LLO to HEO transfer trajectory subdivided into two powered phases and an intermediate coasting phase.

The approximate transfer is constituted by an initial powered phase at constant radius equal to the LLO one, an intermediate Hohmann transfer and a second powered phase at constant radius equal to the HEO apoapsis one.

Parameters

gm (float) – Central body standard gravitational parameter [m^3/s^2]
r (float) – Central body equatorial radius [m]
alt (float) – LLO altitude [m]
rp (float) – HEO periapsis radius [m]
t (float) – HEO period [s]
sc (Spacecraft) – Spacecraft object

Variables

pow1 (PowConstRadius) – PowConstRadius object for the first powered phase
pow2 (PowConstRadius) – PowConstRadius object for the second powered phase
tf (float) – Final time [s]

compute_trajectory(fix_final=False, **kwargs)

Computes the states and controls time series for a given time vector or number of equally space nodes.

Parameters

fix_final (bool, optional) – True if the final angle is fixed, False otherwise. Default is False

Other Parameters

t_eval (ndarray) – Time vector in which states and controls are computed [s]
nb_nodes (int) – Number of equally space nodes in time in which states and controls are computed